Программа Моделирования Химических Процессов
УЧЕБНАЯ ПРОГРАММА КУРСА 'КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ХИМИЧЕСКИХ ПРОЦЕССОВ' Программа составлена кафедрой информатики и компьютерного моделирования, профессором кафедры ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Целью настоящего курса является обучение студентов, занимающихся по программе бакалавров, методам компьютерного химической технологии. Для успешного изучения этой дисциплины студентам к моменту изучения этого курса необходимо освоить три основные группы дисциплин: - компьютеры и вычислительную математику; - неорганическую, аналитическую и физическую химию; - процессы и аппараты химической технологии и общую химическую технологию.
Компьютерные программы для химиков. Мощные пакеты для моделирования химических процессов, графические пакеты для изображения химических формул и диаграмм, пакеты для химических расчетов. Скачать данные программы можно в разделе 'Скачать по химии'. Поэтому курс «Компьютерное моделирование химических процессов» является важнейшей дисциплиной при подготовке студентов в В процессе работы обучающиеся модифицируют под себя уже готовые модельные программы химических процессов на VBA, не затрачивая. Компьютерное моделирование химических процессов. Программа курса. Основные принципы моделирования химических процессов. Физическое и математическое моделирование.
В результате в курсе получают логическое развитие и обобщение методы и приемы расчета процессов, рассмотренные в перечисленных дисциплинах. Курс 'Компьютерное моделирование химических процессов' является общим и изучается студентами всех специальностей университета в 7–8 семестрах. Объем курса составляет 90 часов, из них: лекций – 36 часов, – 54 часа, которые проводятся по схеме: 2+2+4. На самостоятельную работу студентов отводится 72 часа. Монтаж фотографий безплатно. В зависимости от специализации курс завершается зачетом или экзаменом. Курс включает 3 основных раздела.
Построение эмпирических моделей процессов. Математическое моделирование химико-технологических процессов. РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ ПО ОСНОВНЫМ РАЗДЕЛАМ КУРСА Разделы курса Лекции Лабораторные работы Самостоятельная работа 1. Введение 1.1. Основные принципы моделирования химических процессов.
Иерархическая структура химических производств и их математических моделей. Построение эмпирических моделей 2.1. Формулировка задачи аппроксимации для описания экспериментальных зависимостей и получения эмпирических моделей процессов. Нормальный закон распределения для векторных случайных величин и определение их числовых характеристик. Линейный анализ для построения эмпирических моделей на основе данных пассивного эксперимента. Основные положения теории планирования экспериментов: полный факторный эксперимент (ПФЭ) и обработка его результатов.
Активный эксперимент в почти стационарной области в окрестности экстремума функции отклика. Математическое моделирование химико-технологических процессов. Этапы математического моделирования. Разработка математического описания процессов. Математическое моделирование простых гидравлических систем. Математическое моделирование теплообменников с мешалкой и змеевиковых теплообменников в стационарном состоянии.
Программа Моделирования Химических Процессов
Математическое моделирование прямоточных и противоточных трубчатых теплообменников. Математическое моделирование стационарных процессов в реакторах с мешалкой с помощью систем конечных уравнений. Математическое моделирование нестационарных процессов в реакторах с мешалкой с помощью систем обыкновенных уравнений. Явные методы численного (приближенного) решения систем обыкновенных дифференциальных уравнений различных порядков.
Неявные методы численного (приближенного) решения систем обыкновенных дифференциальных уравнений. Математическое моделирование трубчатого реактора в стационарном состоянии с прямоточным движением теплоносителя и с 'ясной кинетической схемой реакции'. 1,5 8 2 3.11.
Математическое моделирование трубчатого реактора в стационарном состоянии с противоточным движением теплоносителя и сложной кинетической схемой реакции. Математическое моделирование нестационарных процессов с распределенными параметрами в трубчатых реакторах с помощью дифференциальных уравнений в частных производных. Математическое моделирование процесса многокомпонентной массопередачи в ректификационных колоннах тарельчатого и насадочного типов.
Оптимизация химико-технологических процессов. 4 4 8 ИТОГО: 36 54 72 СОДЕРЖАНИЕ КУРСА 1. ВВЕДЕНИЕ 1.1. Основные принципы моделирования химических процессов. Физическое и математическое моделирование. Детерминированные и вероятностные математические модели.
Цифровое и аналоговое моделирование. Применение методологии системного анализа для решения задач моделирования.
Применение принципа «черного ящика» при математическом моделировании. Иерархическая структура химических производств и их математических моделей. Основные приемы моделирования: эмпирический, структурный и комбинированный. Построение статических и динамических моделей. Решение прямых задач. Проектный и поверочный ( оценочный ) расчет процессов. Решение обратных задач.
Параметрическая и структурная идентификация математических моделей. Установление адекватности математических моделей. Стратегия проведения расчетных исследований и компьютерного моделирования реальных процессов. Оптимизация химико-технологических процессов. ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ МОДЕЛЕЙ. Формулировка задачи аппроксимации для описания экспериментальных зависимостей и получения эмпирических моделей процессов. Виды критериев аппроксимации.
Критерий метода наименьших квадратов. Решение задачи аппроксимации для нелинейной и линейной по параметрам моделей. Матричная формулировка задачи аппроксимации. Аналитический и алгоритмический подходы для решения задачи аппроксимации для линейных и линеаризованных моделей методом наименьших квадратов. Оценка точности описания с использованием остаточной, а также ошибок и погрешностей в каждой экспериментальной точке измерения. Нормальный закон распределения для векторных случайных величин и определение их числовых характеристик.
Дисперсионный анализ. Определение выборочных коэффициентов корреляции и коэффициента множественной корреляции. Линейный регрессионный анализ для построения эмпирических моделей на основе данных пассивного эксперимента. Понятия функции отклика и факторов. Основные допущения регрессионного анализа. Критерии проверки однородности дисперсий.
Выбор вида уравнений регрессии, определение коэффициентов регрессии и их значимости с использованием критерия Стьюдента. Процедура исключения незначимых коэффициентов регрессии.
Определение адекватности регрессионных моделей с помощью критерия Фишера. Критерий воспроизводимости и условия его применимости. Основные положения теории планирования экспериментов: полный факторный эксперимент (ПФЭ) и обработка его результатов. Оптимальные свойства матрицы планирования и свойство ортогональности.
Определение коэффициентов моделей, их значимости и адекватности уравнения регрессии. Свойство ротатабельности полного факторного эксперимента. Активный эксперимент в почти стационарной области в окрестности экстремума функции отклика. Ортогональный центральный композиционный план эксперимента ( ОЦКП ) и обработка его результатов. Обеспечение ортогональности матрицы планирования и определение величины звездного плеча. Определение коэффициентов модели, их значимости и адекватности уравнения регрессии. Расчетное вычисление координат точки оптимума (экстремума).
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ 3.1. Этапы математического моделирования: формулировка гипотез, построение математического описания, разработка моделирующего алгоритма, проверка адекватности моделей и идентификация их параметров, расчетные исследования (вычислительный эксперимент). Разработка математического описания процессов. Блочный принцип построения структурных математических моделей. Обобщенное описание движения потоков фаз в аппаратах с помощью гидродинамических моделей, учитывающих сосредоточенные и распределенные источники вещества и энергии.
Локальные интенсивности источников вещества и энергии в потоках, соответствующие различным физико-химических процессам. Основные типы уравнений математического описания химико-технологических процессов - конечные, обыкновенные дифференциальные и дифференциальные уравнения в частных производных. Математическое моделирование простых гидравлических систем.
Составление уравнений математического описания процесса в стационарном и нестационарном состоянии. Построение информационных матриц математических моделей для выбора общего алгоритма решения - моделирующего алгоритма. Организация циклических вычислительных процедур и определение корректирующих уравнений. Схематическое изображение моделирующих алгоритмов в виде блок-схем расчетов. Вычислительные, логические и алгоритмические блоки при составлении блок-схем расчетов. Математическое моделирование теплообменников с мешалкой и змеевиковых теплообменников в стационарном состоянии.
Выбор и графическое представление алгоритмов решения. Применение стандартных методов вычислительной математики для решения задачи. Математическое моделирование прямоточных и противоточных трубчатых теплообменников. Решение задачи Коши и краевой задачи. Графическое представление алгоритмов решения. Математическое моделирование стационарных процессов в реакторах с мешалкой с помощью систем конечных уравнений.
Описание микрокинетических закономерностей протекания сложных химических реакций в жикой фазе для многокомпонентных систем. Декомпозиционные алгоритмы решения систем конечных уравнений. Применение метода Ньютона - Рафсона для получения решения.
Проблема сходимости процесса решения. Математическое моделирование нестационарных процессов в реакторах с мешалкой с помощью систем обыкновенных дифференциальных уравнений.
Решение задачи Коши - задачи с начальными условиями. Выбор и графическое представление алгоритма решения. Явные методы численного (приближенного) решения систем обыкновенных дифференциальных уравнений различных порядков - Эйлера, Эйлера-Коши и Рунге-Кутта.
Оценка точности методов - ошибок усечения. Переходные ошибки и ошибки округления при численном интегрировании дифференциальных уравнений.
Способы обеспечения сходимости решения задачи. Неявные методы численного (приближенного) решения систем обыкновенных дифференциальных уравнений - Эйлера и Крэнка-Никольсона (метода трапеций). Применение итерационных алгоритмов решения нелинейных конечных уравнений на каждом шаге интегрирования. Разложение правых частей дифференциальных уравнений в ряды Тейлора для их решения неявным методом Эйлера. Понятие жесткости систем дифференциальных уравнений, критерии жесткости и выбор неявных методов для их решения. Математическое моделирование трубчатого реактора в стационарном состоянии с прямоточным движением теплоносителя и сложной кинетической схемой реакции.
Решение задачи Коши. Графическое представление алгоритма решения. Математическое моделирование трубчатого реактора в стационарном состоянии с противоточным движением теплоносителя и сложной кинетической схемой реакции. Решение краевой задачи.
Графическое представление алгоритма решения. Математическое моделирование нестационарных процессов с распределенными параметрами в трубчатых реакторах с помощью дифференциальных уравнений в частных производных.
Формулировка начальных и граничных условий. Дифференциальные уравнения в частных производных - эллиптического, параболического и гиперболического типов. Алгоритмы решения уравнений параболического типа. Математическая модель химического превращения в изотермических условиях для нестационарного процесса в трубчатых аппаратах с учетом продольного перемешивания. Математическое моделирование процесса многокомпонентной массопередачи в ректификационных колоннах тарельчатого и насадочного типа. Моделирование фазового равновесия и процесса массопередачи на тарелках. Декомпозиционный алгоритм поверочного расчета колонны ректификации.
Оптимизация химико-технологических процессов. Задачи оптимального проектирования и управления. Выбор критериев (целевых функций) и оптимизирующих переменных (ресурсов оптимизации). Ограничения I и II рода. Использование методов оптимизации для решения различных задач: оптимизации процессов с использованием их структурных моделей (численные методы оптимизации процессов) и эмпирических моделей ( экспериментально-статистические методы оптимизации ). ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ЛАБОРАТОРНЫХ РАБОТ 1. Математическое моделирование статических и динамических режимов работы гидравлических систем.
Построение регрессионных моделей зависимостей давлений насыщенных паров индивидуальных веществ от температуры. Построение математических моделей стационарных режимов работы гомогенных жидкофазных реакторов с мешалкой и рубашкой. Построение математических моделей стационарных режимов работы гомогенных жидкофазных трубчатых реакторов. Оптимизация процессов в жидкофазных реакторах с мешалкой. Домашний очаг.:. История:. Окружающий мир:.
Справочная информация.:.:.:.:.:. Техника.:. Образование и наука:. Предметы:.
Программа Моделирования Химических Реакций
Мир:.:. Бизнес и финансы:.:.:.
УТВЕРЖДАЮ Проректор-директор ИПР А. К. Мазуров «»2011 г. РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ НАПРАВЛЕНИЕ ООП 241000 Энерго- и ресурсосберегающие процессы химической технологии нефтехимии и биотехнологии ПРОФИЛИ ПОДГОТОВКИ: Основные процессы химических производств и химическая кибернетика КВАЛИФИКАЦИЯ бакалавр БАЗОВЫЙ УЧЕБНЫЙ ПЛАН ПРИЕМА 2011 г. КУРС 4 СЕМЕСТР 7 КОЛИЧЕСТВО КРЕДИТОВ 6 (5/4) ПРЕРЕКВИЗИТЫ Б2.Б1, Б2.В1.1, Б2.Б6, Б3.Б4 КОРЕКВИЗИТЫ Б3В1.6, Б3В1.7 ВИДЫ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ И ВРЕМЕННОЙ РЕСУРС: Лекции 36 час. Практические занятия Лабораторные занятия 54 час. АУДИТОРНЫЕ ЗАНЯТИЯ 90 час.
САМОСТОЯТЕЛЬНАЯ РАБОТА 72 час. ИТОГО 162 час. ФОРМА ОБУЧЕНИЯ очная ВИД ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ экзамен (7) ОБЕСПЕЧИВАЮЩЕЕ ПОДРАЗДЕЛЕНИЕ кафедра ХТТ и ХК ЗАВЕДУЮЩИЙ КАФЕДРОЙ А. В. Кравцов РУКОВОДИТЕЛЬ ООП Н.В. Ушева ПРЕПОДАВАТЕЛЬ Н. В. Ушева 2011 г.
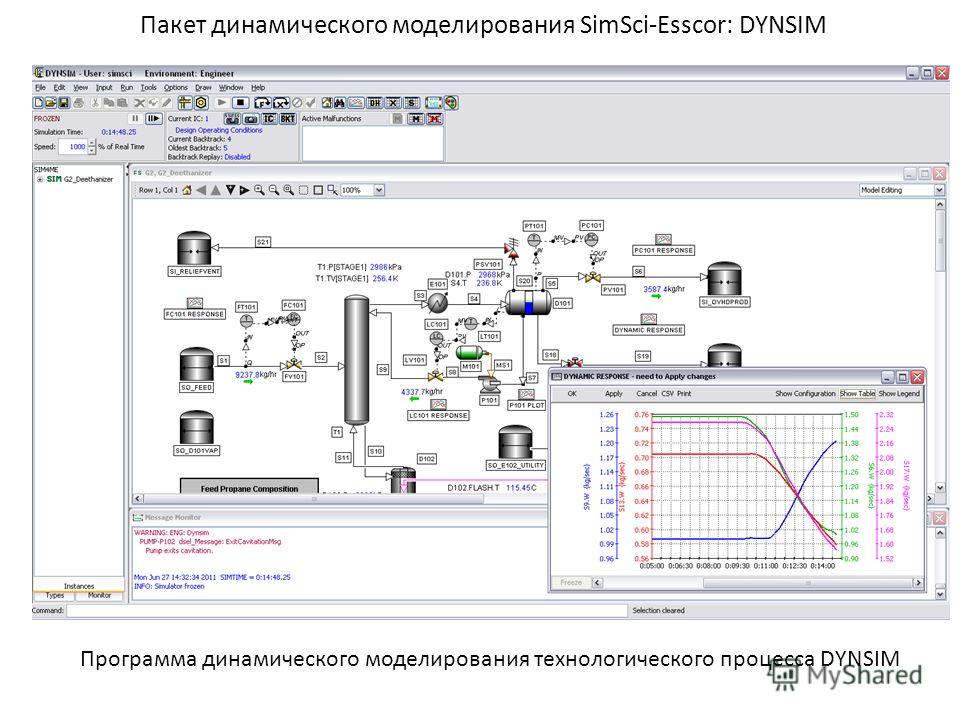
Цели освоения дисциплины Цели дисциплины и их соответствие целям ООП Код цели Цели освоения дисциплины «Математическое моделирование химико-технологических процессов» Цели ООП Ц1 Применять математическое моделирование при анализе, оптимизации и оценке ресурсоэффективности химико-технологических процессов. Подготовка выпускников к производственно-технологической деятельности в области энерго- и ресурсосберегающих процессов в химической технологии, нефтехимии и биотехнологии, конкурентоспособных на мировом рынке. Ц2 Формирование способности выполнять расчеты химико-технологических процессов с использованием математических моделей, моделирующих систем и современных прикладных программ Подготовка выпускников к проектной деятельности в области энерго- и ресурсосберегающих процессов в химической технологии, нефтехимии и биотехнологии. Ц3 Применение знаний физико-химической сущности процессов и методологии математического моделирования, при проведении научных исследований.
Подготовка выпускников к научным исследованиям для решения задач, связанных с разработкой новых методов создания процессов, материалов и оборудования, обеспечивающих энерго-ресурсосбережение, экологическую безопасность технологи. Ц5 Формирование навыков самостоятельного проведения теоретических и экспериментальных исследований с использованием современных компьютерных технологий Подготовка выпускников к самообучению и непрерывному профессиональному самосовершенствованию 2. Место дисциплины в структуре ООП Согласно ФГОС и ООП «Энерго- и ресурсосберегающие процессы химической технологии, нефтехимии и биотехнологии» дисциплина «Математическое моделирование химико-технологических процессов» является базовой дисциплиной и относится к технологическому модулю. Код дисциплины ООП Наименование дисциплины Кредиты Форма контроля Модуль Б.Б. 2.1 (технологический) Базовая часть Б3.В1.4 Моделирование ХТП 7 экзамен До освоения дисциплины «Математическое моделирование химико-технологических процессов » должны быть изучены следующие дисциплины (пререквизиты): Код дисциплины ООП Наименование дисциплины Кредиты Форма контроля пререквизиты Модуль Б.
1 (математический) Б2.Б1 Математика 12 экзамен Б2.В1.1 Информатика 8 экзамен Модуль Б. 3 (химический) Б2.Б6 Физическая химия 6 экзамен Модуль Б.3.2 (технологический) Б3.Б4 Процессы и аппараты химической технологии 14 Дифф. Зачет,Экзамен кореквизиты Б3.В1.6 Переработка нефти и газа 8 Экзамен Б3.В1.6 Методы кибернетики ХТП 6 Экзамен При изучении указанных дисциплин (пререквизитов) формируются «входные» знания, умения, опыт и компетенции, необходимые для успешного освоения дисциплины «Математическое моделирование ХТП».